Demography Informal Methods Seminar - Population Projection and the Lee-Carter Model
Population Projection
- One of the most fundamental forms of demographic analysis
- Uses age-structured rates of fertility and mortality to project the population structure forward into time
- Shows patterns of population growth and age composition in future populations
- Further analysis can show population growth rates and sensitivity of the growth rate to the vital rates
Methods
- Cohort component method
- \[P_{t+n} = P_t + B_t - D_t + M_t\]
- Hamilton-Perry method
- Very low data requirements
- Uses cohort change ratios from two previous censuses to project the population forward
- \[P_{t+n} = CCR_{t, t-n} * P_t\] Where the \(CCR\) is the ratio of the population age structure at the two previous censuses.
- Good description is here and here
Original article here
- Leslie Matrix model Leslie, 1945
- Birth Pulse model
- People reproduce at specific ages after surviving to that age
Very thorough treatment in Keyfitz and Caswell, 2005, Chapters 3, 7 and 9
\[\begin{pmatrix} n_1\\ n_2\\ n_3 \end{pmatrix} (t+1)= \begin{pmatrix} F_1 & F_2 & F_3\\ P_1 & 0 & 0\\ 0 & P_2 & 0 \end{pmatrix} \begin{pmatrix} n_1\\ n_2\\ n_3 \end{pmatrix}(t)\]
Or as: \[n(t+1) = \mathbf{A} n(t)\]
\(n_k\) are the population sizes, \(F_k\) are the reproductive values at each age, and \(P_k\) are the survivorship ratios at each age
- Very flexible - accomodates both age and stage structure, more general population model than cohort component
- Bayesian projection methods
- Bayespop
- Uses methods from Bayesian statistics to project TFR, \(e_0\) and population structure
- Incorporates uncertainty in all levels of analysis
- Leads to projections with errors incorporated
- Used by the UN Population Division
Example - Leslie Matrix Model
Below, I will illustrate how to use data from the Human Mortality Database and the Human Fertility Database for the US to create a Leslie Matrix model.
## ── Attaching packages ─────────────────────────────────────────────────────────────── tidyverse 1.3.0 ──## ✓ ggplot2 3.3.2 ✓ purrr 0.3.4
## ✓ tibble 3.0.3 ✓ dplyr 1.0.0
## ✓ tidyr 1.1.0 ✓ stringr 1.4.0
## ✓ readr 1.3.1 ✓ forcats 0.5.0## ── Conflicts ────────────────────────────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()Data from HMD/HFD
The human mortality and human fertility databases are excellent sources for national historic series of mortality and fertility rates. You need to register with them to get access to the data.
UShmd<- readHMDweb(CNTRY = "USA", item ="fltper_5x5", password =mypassword,username = myusername)
#49 for item, 51 for US
us_mort<-UShmd%>%
filter(Year == 2015)
#average qx and lx for ages 0 to 1 and 1 to 4
us_mort$qx[us_mort$Age==0]<-us_mort$qx[us_mort$Age==0]+us_mort$qx[us_mort$Age==1]
us_mort$Lx[us_mort$Age==0]<-us_mort$Lx[us_mort$Age==0]+us_mort$Lx[us_mort$Age==1]
us_mort<-us_mort[-2,]
head(us_mort)## Year Age mx qx ax lx dx Lx Tx ex OpenInterval
## 1 2015 0 0.00530 0.00615 0.14 100000 527 497227 8135585 81.36 FALSE
## 3 2015 5 0.00011 0.00053 2.40 99386 53 496790 7638358 76.86 FALSE
## 4 2015 10 0.00012 0.00061 2.81 99332 61 496529 7141568 71.90 FALSE
## 5 2015 15 0.00029 0.00147 2.85 99271 146 496043 6645039 66.94 FALSE
## 6 2015 20 0.00049 0.00246 2.61 99125 243 495045 6148996 62.03 FALSE
## 7 2015 25 0.00066 0.00329 2.61 98882 325 493632 5653951 57.18 FALSEFertility data are by single year of age, so I aggregate to 5 year intervals
UShfd<-readHFDweb(CNTRY="USA",username = myusername,password =myotherpassword, item = "asfrRR")
#30
us_fert<-UShfd%>%
filter(Year==2015)%>%
mutate(age_grp = cut(Age, breaks = seq(10, 55, 5), include.lowest = T))%>%
group_by(age_grp)%>%
summarise(asfr5 = sum(ASFR))%>%
filter(is.na(age_grp)==F)%>%
ungroup()## `summarise()` ungrouping output (override with `.groups` argument)## # A tibble: 6 x 3
## age_grp asfr5 age5
## <fct> <dbl> <dbl>
## 1 [10,15] 0.0049 10
## 2 (15,20] 0.171 15
## 3 (20,25] 0.414 20
## 4 (25,30] 0.543 25
## 5 (30,35] 0.469 30
## 6 (35,40] 0.205 35Combine these together
us_dem<-merge(us_mort, us_fert, by.x="Age", by.y="age5", all.x=T)
us_dem$asfr5<-ifelse(is.na(us_dem$asfr5)==T, 0, us_dem$asfr5)
head(us_dem)## Age Year mx qx ax lx dx Lx Tx ex OpenInterval
## 1 0 2015 0.00530 0.00615 0.14 100000 527 497227 8135585 81.36 FALSE
## 2 5 2015 0.00011 0.00053 2.40 99386 53 496790 7638358 76.86 FALSE
## 3 10 2015 0.00012 0.00061 2.81 99332 61 496529 7141568 71.90 FALSE
## 4 15 2015 0.00029 0.00147 2.85 99271 146 496043 6645039 66.94 FALSE
## 5 20 2015 0.00049 0.00246 2.61 99125 243 495045 6148996 62.03 FALSE
## 6 25 2015 0.00066 0.00329 2.61 98882 325 493632 5653951 57.18 FALSE
## age_grp asfr5
## 1 <NA> 0.00000
## 2 <NA> 0.00000
## 3 [10,15] 0.00490
## 4 (15,20] 0.17101
## 5 (20,25] 0.41403
## 6 (25,30] 0.54271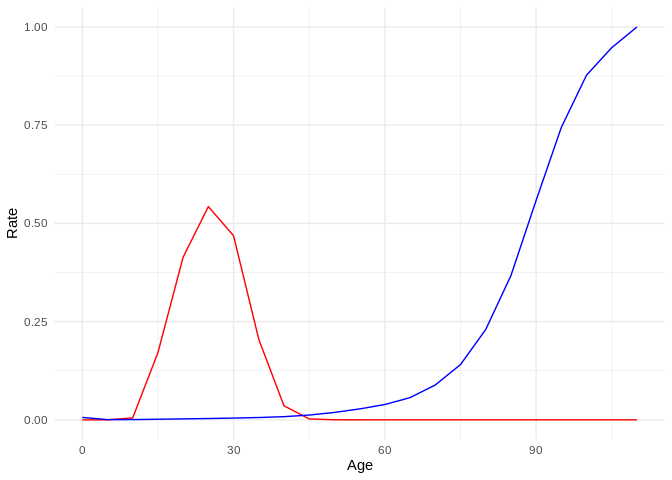
Population data
I get the 2015 population age distribution from the census estimates using tidycensus You can see the various parameters here
us_popn<-get_estimates(geography="us", product = "characteristics", breakdown = c("AGEGROUP", "SEX"), year = 2015)
us_popn<-us_popn%>%
filter(AGEGROUP>0&AGEGROUP<19, SEX==2)%>%
#mutate(case_when(.$AGEGROUP==1))%>%
arrange(AGEGROUP)
head(us_popn)## # A tibble: 6 x 5
## GEOID NAME value AGEGROUP SEX
## <chr> <chr> <dbl> <dbl> <dbl>
## 1 1 United States 9729680 1 2
## 2 1 United States 10028044 2 2
## 3 1 United States 10101942 3 2
## 4 1 United States 10311036 4 2
## 5 1 United States 11071459 5 2
## 6 1 United States 11052155 6 2Leslie Matrix Construction
- Need matrix \(A\), that is # of ages by # of ages in size, in this case, it will be 18 x 18
- The first row are the reproductive values, \(F_k\) THESE ARE NOT AGE SPECIFIC FERTILITY RATES, they also have to incorporate the probability of surviving to the age of reproduction.
\[F_k = l(.5) \left ( \frac{m_i+P_i m_{i+1}}{2} \right)\]
The *sub-diagonal is the survival ratios, these are calculated as \(L_{x+1}/L_{x})\)
Another note is that this is a one-sex population model, in this case, for females only.
I use code from Eddie Hunsinger’s Leslie Matrix Code, so the good ideas here belong to him.
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## [1,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [2,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [3,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [4,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [5,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [6,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [7,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [8,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [9,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [10,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [11,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [12,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [13,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [14,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [15,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [16,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [17,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [18,] 0 0 0 0 0 0 0 0 0 0 0 0 0
## [,14] [,15] [,16] [,17] [,18]
## [1,] 0 0 0 0 0
## [2,] 0 0 0 0 0
## [3,] 0 0 0 0 0
## [4,] 0 0 0 0 0
## [5,] 0 0 0 0 0
## [6,] 0 0 0 0 0
## [7,] 0 0 0 0 0
## [8,] 0 0 0 0 0
## [9,] 0 0 0 0 0
## [10,] 0 0 0 0 0
## [11,] 0 0 0 0 0
## [12,] 0 0 0 0 0
## [13,] 0 0 0 0 0
## [14,] 0 0 0 0 0
## [15,] 0 0 0 0 0
## [16,] 0 0 0 0 0
## [17,] 0 0 0 0 0
## [18,] 0 0 0 0 0size<-dim(A)[1]
sxf1<-array(0,c(size-1))
Lxf<-us_dem$Lx/100000
for (i in 1:size-1){sxf1[i]<-(Lxf[i+1]/Lxf[i])}
#make matrix with survivals on off diagonal
sf1<-rbind(0,cbind(diag(sxf1),0))
##SPECIAL CALCULATION FOR OPEN-ENDED AGE GROUP OF LESLIE MATRICES
sf1[size,size]<-sf1[size,size-1]<-Lxf[size]/(Lxf[size]+Lxf[size-1])
# proportion of female births
ffab<-0.4882846
##MAKE THE LESLIE MATRICES FOR FEMALES
#convert fertilities to proportions
fert<-us_dem$asfr5#/sum(us_dem$asfr5)
##Make first row of matrix - reproductive values
for(j in 1:size-1)
{sf1[1,j]<-(Lxf[1]/10)*(fert[j]+fert[j+1]*(sxf1[j]))*ffab}
sf1## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 0.0000000 0.001189038 0.04266825 0.1418386 0.2319092 0.2450830 0.1632889
## [2,] 0.9991211 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [3,] 0.0000000 0.999474627 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [4,] 0.0000000 0.000000000 0.99902121 0.0000000 0.0000000 0.0000000 0.0000000
## [5,] 0.0000000 0.000000000 0.00000000 0.9979881 0.0000000 0.0000000 0.0000000
## [6,] 0.0000000 0.000000000 0.00000000 0.0000000 0.9971457 0.0000000 0.0000000
## [7,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.9961611 0.0000000
## [8,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.9948631
## [9,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [10,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [11,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [12,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [13,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [14,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [15,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [16,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [17,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [18,] 0.0000000 0.000000000 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000
## [,8] [,9] [,10] [,11] [,12] [,13]
## [1,] 0.05840419 0.009203672 0.0005699971 3.641824e-05 0.0000000 0.0000000
## [2,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [3,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [4,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [5,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [6,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [7,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [8,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [9,] 0.99317268 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [10,] 0.00000000 0.990100253 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [11,] 0.00000000 0.000000000 0.9847503747 0.000000e+00 0.0000000 0.0000000
## [12,] 0.00000000 0.000000000 0.0000000000 9.768769e-01 0.0000000 0.0000000
## [13,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.9669513 0.0000000
## [14,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.9531395
## [15,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [16,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [17,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [18,] 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.0000000 0.0000000
## [,14] [,15] [,16] [,17] [,18]
## [1,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [2,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [3,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [4,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [5,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [6,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [7,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [8,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [9,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [10,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [11,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [12,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [13,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [14,] 0.000000 0.0000000 0.000000 0.0000000 0.0000000
## [15,] 0.928972 0.0000000 0.000000 0.0000000 0.0000000
## [16,] 0.000000 0.8878485 0.000000 0.0000000 0.0000000
## [17,] 0.000000 0.0000000 0.819659 0.0000000 0.0000000
## [18,] 0.000000 0.0000000 0.000000 0.4147917 0.4147917#assemble matrix
sf1[size,size]<-0
A<-sf1
plot(x=seq(0, 80, 5), y=diag(sf1[-1,-ncol(sf1)]), type="l", ylim=c(0, 1), ylab="Rate", xlab="Age")
lines(x=seq(0, 80, 5), y = sf1[1, -size], col=2)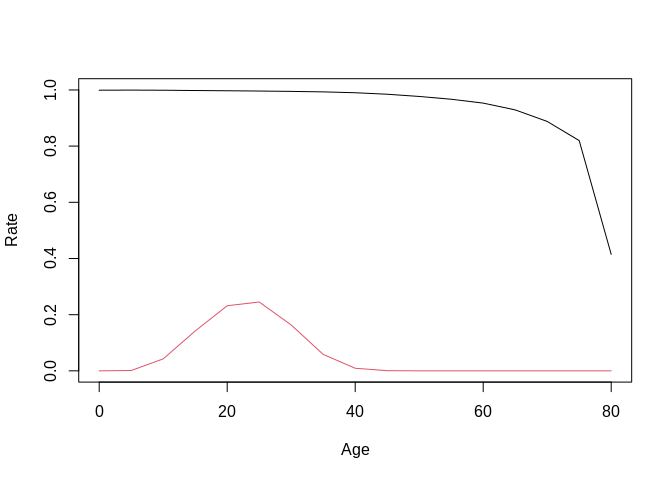
Project the population
Since these data represent 5 year age intervals, the projections will move the population forward in increments of 5 years. Below, I project the population forward by 10 periods, or 50 years. Given that we start at 2015 using data from the HMD/HFD, this will take us to 2065.
The weakness of this model is that it does not incorporate migration, so this is an incomplete model, but reflects the extrapolation of the population using current and unchanging rates of fertility and mortality. The model can be expanded to incorporate segmented populations, however, with exchanges between areas.
##MAKE ARRAYS TO HOLD THE DATA
nproj<-10
newpop<-matrix(0, nrow=size, ncol=nproj)
newpop[,1]<-us_popn$value #first column is current population size
#loop over the new periods
for(i in 2:nproj){
newpop[,i]<-(A%*%newpop[,i-1])}
head(newpop)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 9729680 9638886 9486594 9236391 8992077 8801727 8641051 8481188
## [2,] 10028044 9721129 9630414 9478257 9228274 8984174 8793992 8633456
## [3,] 10101942 10022776 9716022 9625355 9473277 9223425 8979454 8789372
## [4,] 10311036 10092054 10012965 9706512 9615934 9464005 9214397 8970665
## [5,] 11071459 10290291 10071750 9992820 9686983 9596587 9444964 9195859
## [6,] 11052155 11039858 10260920 10043002 9964298 9659333 9569196 9418005
## [,9] [,10]
## [1,] 8310317 8126435
## [2,] 8473734 8303014
## [3,] 8628921 8469282
## [4,] 8780769 8620475
## [5,] 8952617 8763102
## [6,] 9169611 8927063#Plot the new total population sizes
options(scipen=999)
plot(y = apply(newpop, 2, sum), x= seq(2015, 2060, 5) , main="Total Female Population Size to 2060")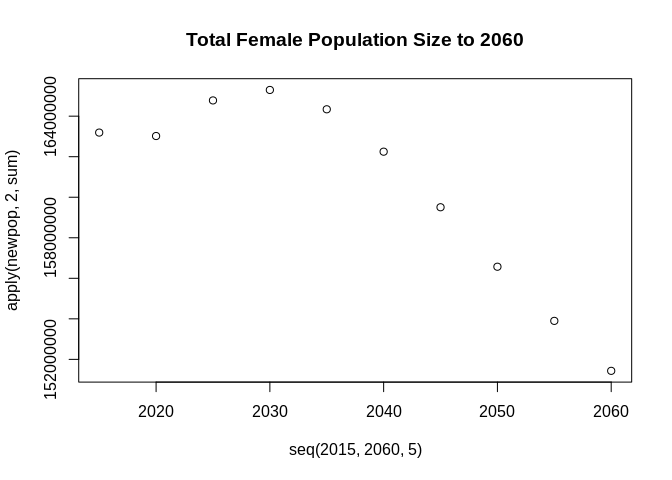
Further analysis of the matrix…
See Jamie’s Notes and Ch 13 of Keyfitz and Caswell for more details on this.
We can do a eigenvalue decomposition of the matrix \(A\), and recover the population growth rate from the log of the first eigenvalue. The stable age structure can also be recovered by the standardized first eigenvector of the matrix.
## [1] 0.9791456+0i## [1] -0.02107494+0i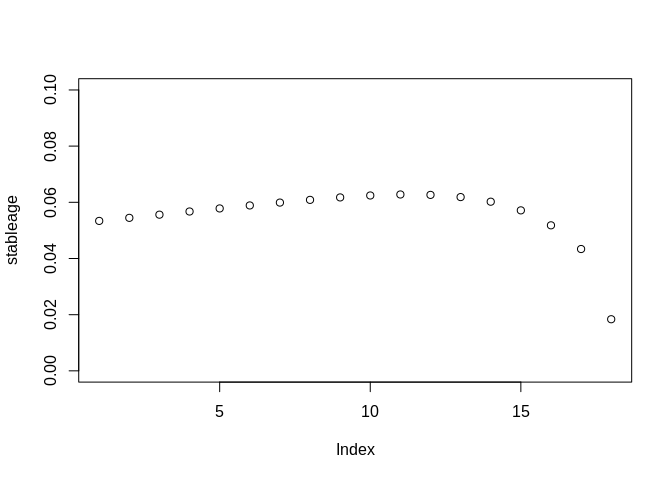
Even more analysis….
library(demogR)
A2<-leslie.matrix(lx=us_dem$lx/100000, mx=us_dem$asfr5, one.sex = T, SRB = 1.048, infant.class = F)
ea<-eigen.analysis(A2)
ea## $lambda1
## [1] 0.9788133
##
## $rho
## [1] 2.393615
##
## $sensitivities
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.0000000 0.09003766 0.09193005 0.09378177 0.09557683 0.09732468
## [2,] 0.3475641 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## [3,] 0.0000000 0.17304440 0.00000000 0.00000000 0.00000000 0.00000000
## [4,] 0.0000000 0.00000000 0.16532057 0.00000000 0.00000000 0.00000000
## [5,] 0.0000000 0.00000000 0.00000000 0.13875608 0.00000000 0.00000000
## [6,] 0.0000000 0.00000000 0.00000000 0.00000000 0.09429642 0.00000000
## [7,] 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.04638306
## [8,] 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## [9,] 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## [10,] 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## [11,] 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## [,7] [,8] [,9] [,10] [,11]
## [1,] 0.0989884 0.100539402 0.1018889841 0.102833546869 0.103081
## [2,] 0.0000000 0.000000000 0.0000000000 0.000000000000 0.000000
## [3,] 0.0000000 0.000000000 0.0000000000 0.000000000000 0.000000
## [4,] 0.0000000 0.000000000 0.0000000000 0.000000000000 0.000000
## [5,] 0.0000000 0.000000000 0.0000000000 0.000000000000 0.000000
## [6,] 0.0000000 0.000000000 0.0000000000 0.000000000000 0.000000
## [7,] 0.0000000 0.000000000 0.0000000000 0.000000000000 0.000000
## [8,] 0.0138569 0.000000000 0.0000000000 0.000000000000 0.000000
## [9,] 0.0000000 0.002021231 0.0000000000 0.000000000000 0.000000
## [10,] 0.0000000 0.000000000 0.0001265769 0.000000000000 0.000000
## [11,] 0.0000000 0.000000000 0.0000000000 0.000007694781 0.000000
## attr(,"class")
## [1] "leslie.matrix"
##
## $elasticities
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.0000000 0.0002192746 0.00803085 0.0272386 0.04539112 0.04884489
## [2,] 0.1769007 0.0000000000 0.00000000 0.0000000 0.00000000 0.00000000
## [3,] 0.0000000 0.1766814188 0.00000000 0.0000000 0.00000000 0.00000000
## [4,] 0.0000000 0.0000000000 0.16865057 0.0000000 0.00000000 0.00000000
## [5,] 0.0000000 0.0000000000 0.00000000 0.1414120 0.00000000 0.00000000
## [6,] 0.0000000 0.0000000000 0.00000000 0.0000000 0.09602085 0.00000000
## [7,] 0.0000000 0.0000000000 0.00000000 0.0000000 0.00000000 0.04717596
## [8,] 0.0000000 0.0000000000 0.00000000 0.0000000 0.00000000 0.00000000
## [9,] 0.0000000 0.0000000000 0.00000000 0.0000000 0.00000000 0.00000000
## [10,] 0.0000000 0.0000000000 0.00000000 0.0000000 0.00000000 0.00000000
## [11,] 0.0000000 0.0000000000 0.00000000 0.0000000 0.00000000 0.00000000
## [,7] [,8] [,9] [,10] [,11]
## [1,] 0.03310194 0.012025654 0.0019206122 0.000120037015 0.000007713299
## [2,] 0.00000000 0.000000000 0.0000000000 0.000000000000 0.000000000000
## [3,] 0.00000000 0.000000000 0.0000000000 0.000000000000 0.000000000000
## [4,] 0.00000000 0.000000000 0.0000000000 0.000000000000 0.000000000000
## [5,] 0.00000000 0.000000000 0.0000000000 0.000000000000 0.000000000000
## [6,] 0.00000000 0.000000000 0.0000000000 0.000000000000 0.000000000000
## [7,] 0.00000000 0.000000000 0.0000000000 0.000000000000 0.000000000000
## [8,] 0.01407402 0.000000000 0.0000000000 0.000000000000 0.000000000000
## [9,] 0.00000000 0.002048363 0.0000000000 0.000000000000 0.000000000000
## [10,] 0.00000000 0.000000000 0.0001277503 0.000000000000 0.000000000000
## [11,] 0.00000000 0.000000000 0.0000000000 0.000007713299 0.000000000000
## attr(,"class")
## [1] "leslie.matrix"
##
## $stable.age
## [1] 0.15344201 0.07809782 0.07973927 0.08134544 0.08290245 0.08441852
## [7] 0.08586161 0.08720694 0.08837755 0.08919686 0.08941152
##
## $repro.value
## [1] 1.00000000000 1.96474122445 1.92191138920 1.79832990425 1.47956336158
## [6] 0.98660333067 0.47658070739 0.13998508461 0.02010386664 0.00124230193
## [11] 0.00007482753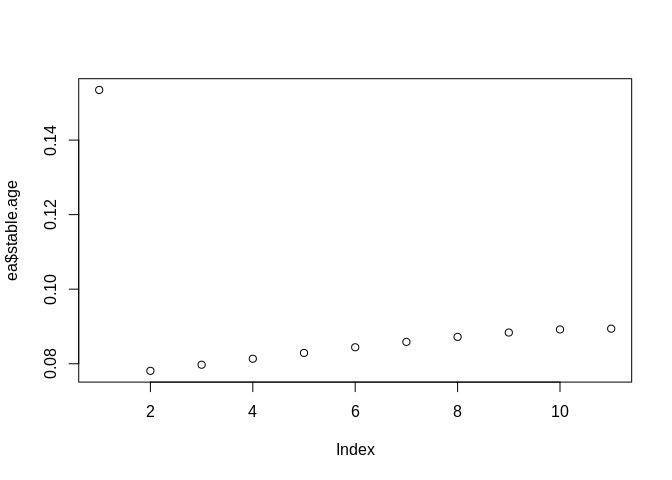
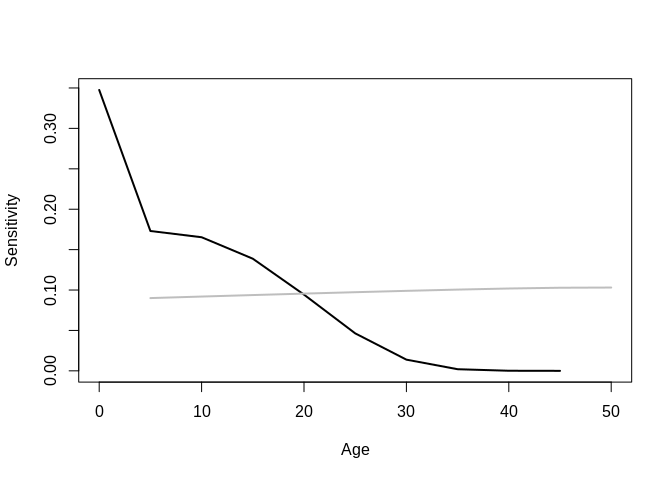
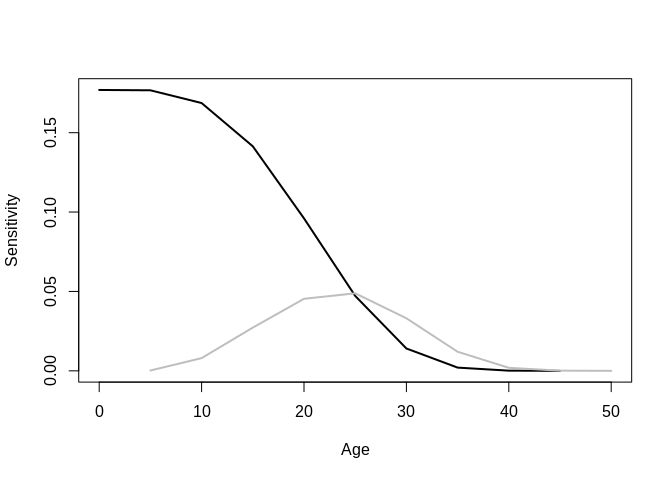
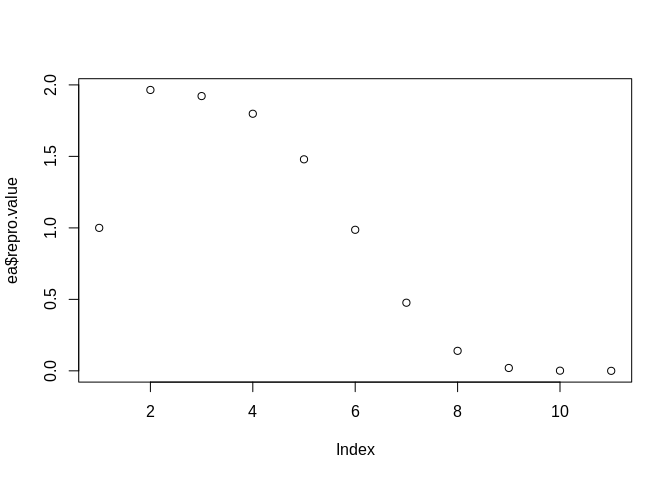
While this may seem strange, there are other analyses that show a decline in the US population in the absence of migration. Also see this report in the Washington Post.
Lee-Carter Method for Mortality Forecasting
This method originates with Lee & Carter, 1992
They describe a method of forecasting age-specific mortality rates. Their method takes a series of age-specific mortality rates and writes it as a decomposition into an age specific average mortality, a vector of age specific changes in mortality and a period level vector of mortality trends.
\[ln(m_{x,t} = \alpha_x + \beta_x k_t +\epsilon_{x,t})\]
The solution to this equation comes from an eigenvalue decomposition of the \(m_{x,t}\) matrix. Several additions and extensions of the method have been published over the years, and is an active area of research.
## Loading required package: forecast## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo## Registered S3 methods overwritten by 'demography':
## method from
## print.lca e1071
## summary.lca e1071## This is demography 1.22## Loading required package: gnm## Loading required package: rainbow## Loading required package: MASS##
## Attaching package: 'MASS'## The following object is masked from 'package:dplyr':
##
## select## Loading required package: pcaPP## Loading required package: RCurl##
## Attaching package: 'RCurl'## The following object is masked from 'package:tidyr':
##
## completedata
Again, get data from the HMD, here for the US Don’t use my password!!
## Warning in hmd.mx(country = "USA", username = myusername, password =
## mypassword, : NAs introduced by coercionusdat<-extract.years(usdat, years=1940:2017)
#male data
usdatm<-demogdata(data=usdat$rate$male,pop=usdat$pop$male,ages = usdat$age,years=usdat$year,label = usdat$label,name="male", type="mortality")
#Female data
usdatf<-demogdata(data=usdat$rate$female,pop=usdat$pop$female,ages = usdat$age,years=usdat$year,label = usdat$label,name="female", type="mortality")
summary(usdatf)## Mortality data for USA
## Series: female
## Years: 1940 - 2017
## Ages: 0 - 110Fit Lee - Carter model
I use the highest age as 90
## Lee-Carter analysis
##
## Call: lca(data = usdatm, max.age = 90)
##
## Adjustment method: dt
## Region: USA
## Years in fit: 1940 - 2017
## Ages in fit: 0 - 90
##
## Percentage variation explained: 94.8%
##
## ERROR MEASURES BASED ON MORTALITY RATES
##
## Averages across ages:
## ME MSE MPE MAPE
## 0.00008 0.00001 0.00889 0.07006
##
## Averages across years:
## IE ISE IPE IAPE
## 0.00735 0.00044 0.79566 6.25470
##
##
## ERROR MEASURES BASED ON LOG MORTALITY RATES
##
## Averages across ages:
## ME MSE MPE MAPE
## 0.00435 0.00918 -0.00074 0.01394
##
## Averages across years:
## IE ISE IPE IAPE
## 0.39110 0.81147 -0.06745 1.23020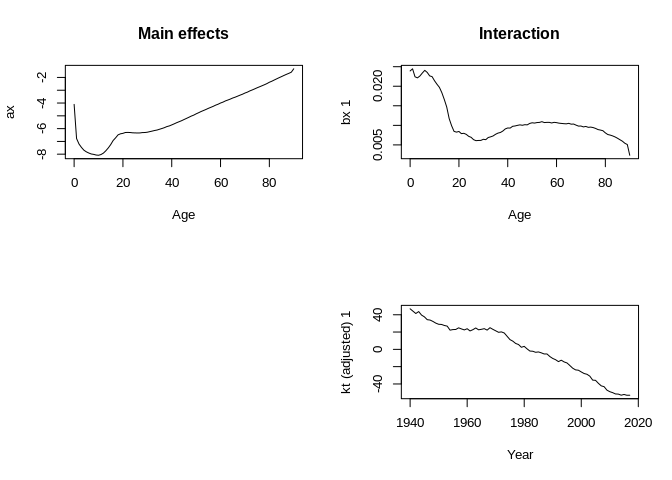
plot(x=lca1$age, y=log(lca1$male[,1]), type="l", lty=1,
main="Observed vs fitted Lee Carter Model - 1940 and 2017 Male Mortality",
ylim=c(-10, 0))
lines(lca1$age, y=lca1$fitted$y[,1],
col=1, lty=2)
lines(x=lca1$age, y=log(lca1$male[,78]), col=3)
lines(lca1$age, y=lca1$fitted$y[,78],
col=3, lty=2)
legend("top", legend=c("Obs 1940", "Pred 1940", "Obs 2017", "Pred 2017"), col=c(1,1,3,3), lty=c(1,2,1,2))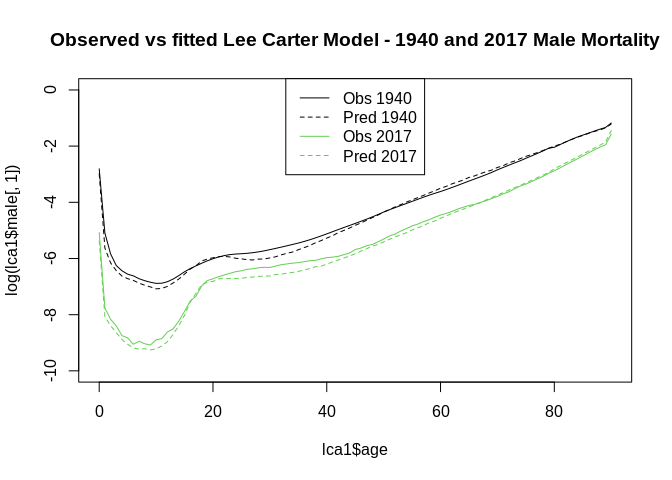
## Lee-Carter analysis
##
## Call: lca(data = usdatf, max.age = 90)
##
## Adjustment method: dt
## Region: USA
## Years in fit: 1940 - 2017
## Ages in fit: 0 - 90
##
## Percentage variation explained: 96.1%
##
## ERROR MEASURES BASED ON MORTALITY RATES
##
## Averages across ages:
## ME MSE MPE MAPE
## 0.00001 0.00000 0.00485 0.06322
##
## Averages across years:
## IE ISE IPE IAPE
## 0.00076 0.00025 0.43738 5.65090
##
##
## ERROR MEASURES BASED ON LOG MORTALITY RATES
##
## Averages across ages:
## ME MSE MPE MAPE
## 0.00080 0.00820 -0.00002 0.01114
##
## Averages across years:
## IE ISE IPE IAPE
## 0.07162 0.73168 -0.00215 0.98433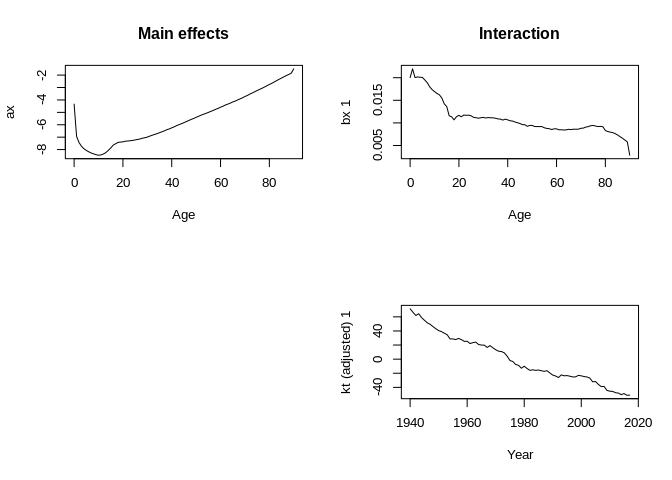
plot(x=lca2$age, y=log(lca2$female[,1]), type="l", lty=1,
main="Observed vs fitted Lee Carter Model - 1940 and 2017 Female Mortality",
ylim=c(-10, 0))
lines(lca2$age, y=lca2$fitted$y[,1],
col=1, lty=2)
lines(x=lca2$age, y=log(lca2$female[,78]), col=3)
lines(lca2$age, y=lca2$fitted$y[,78],
col=3, lty=2)
legend("top", legend=c("Obs 1940", "Pred 1940", "Obs 2017", "Pred 2017"), col=c(1,1,3,3), lty=c(1,2,1,2))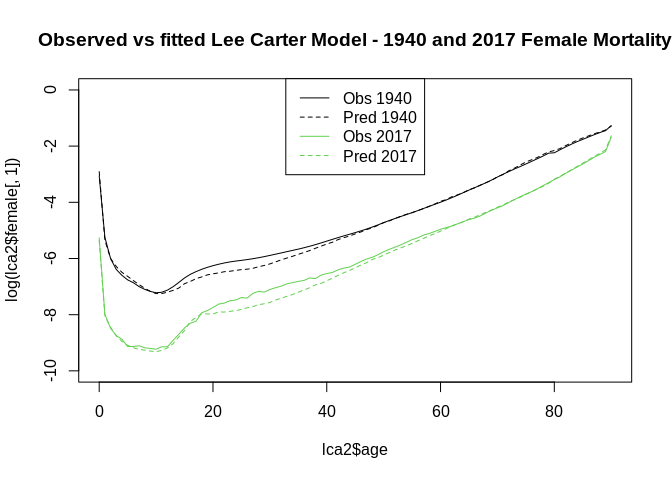
#par(mfrow=c(1,2))
plot(usdatm,years=1940:2017,ylim=c(-11,1), ages = 60:90, main="Males - Ages 60 - 90")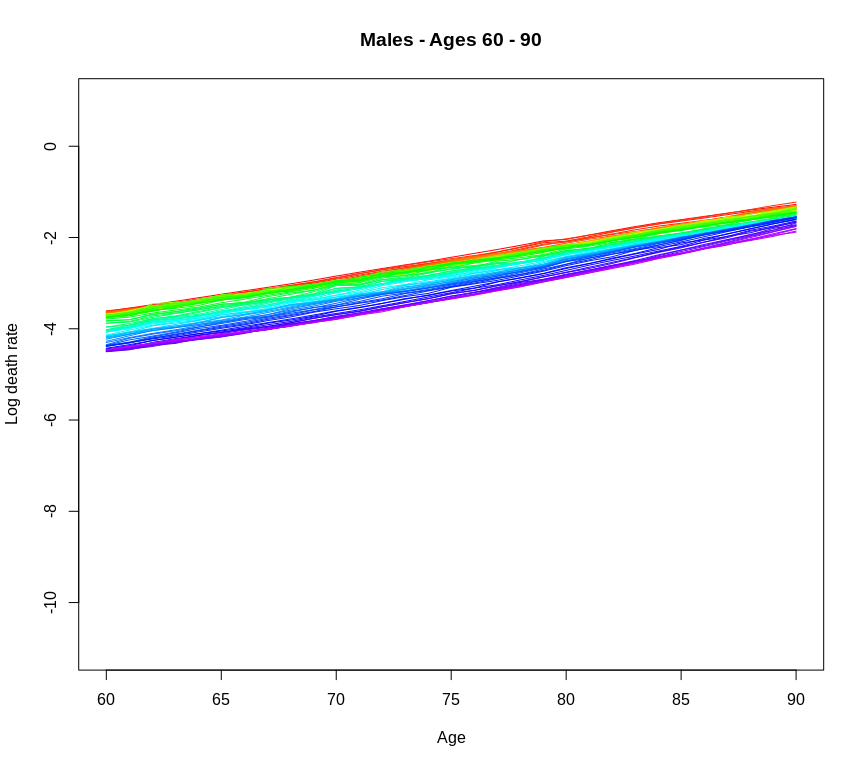
out1<-forecast(lca1,h=20)
plot(usdatf,years=1940:2017,ylim=c(-11,1), ages = 60:90, main="Females - Ages 60 - 90")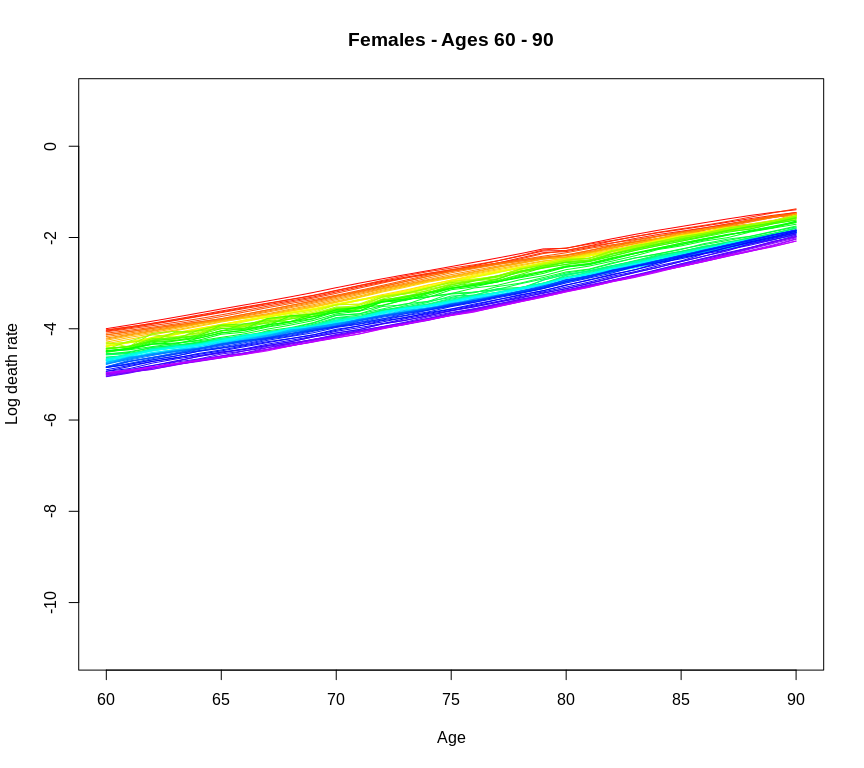
out2<-forecast(lca2,h=20)
par(mfrow=c(2,1))
plot(forecast(lca1,h=20,jumpchoice="fit"),ylim=c(-11,1) )
lines(log(lca1$male[, 1]))
plot(forecast(lca2,h=20,jumpchoice="fit"),ylim=c(-11,1))
lines(lca2$female[, 1])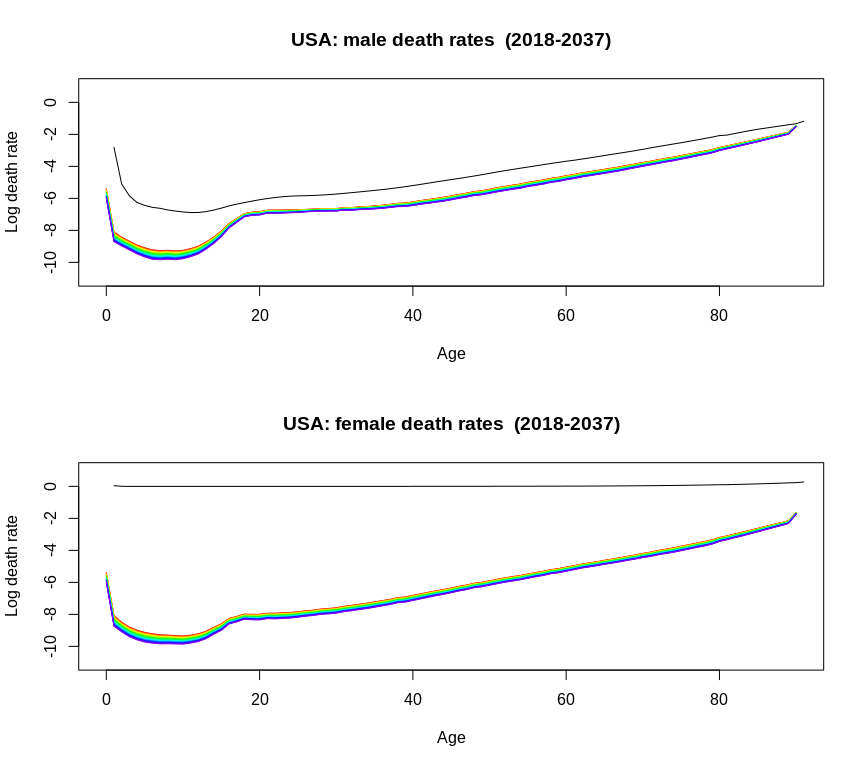
Mechanics of Lee - Carter
I got this example largely from here. It uses the StMoMo library. You should also totally check out this video by the author of that package, as to how great it is, also as to why it’s called StMoMo.
## Warning in hmd.mx(country = "USA", username = myusername, password =
## mypassword, : NAs introduced by coercionusdat2_m <- StMoMoData(usdat2,series = "male")
usdat2_f <- StMoMoData(usdat2,series = "female")
Years <- usdat2$year
Age <- usdat2$age
m <- usdat2$rate$male
m <- log(m)
n.x = nrow(m) # 111
n.y = ncol(m) #78
m_mat <- matrix(m, nrow = n.x, ncol = n.y) # 111 X 85
plot(x=Age, y=m_mat[,1], type = "l", ylim=c(-10, 0), ylab="log rate") #mortality of all ages in year 1940
# Mean log mortality for all age groups under consideration (Age)
a_age <- rowMeans(m_mat)
lines(x = Age, y = a_age, col = 2)#average mortality for all age groups
legend("topleft", legend=c("1940 Mortality - M - Obs","Average Mortality - Male"), col=c(1,2), lty=c(1,1))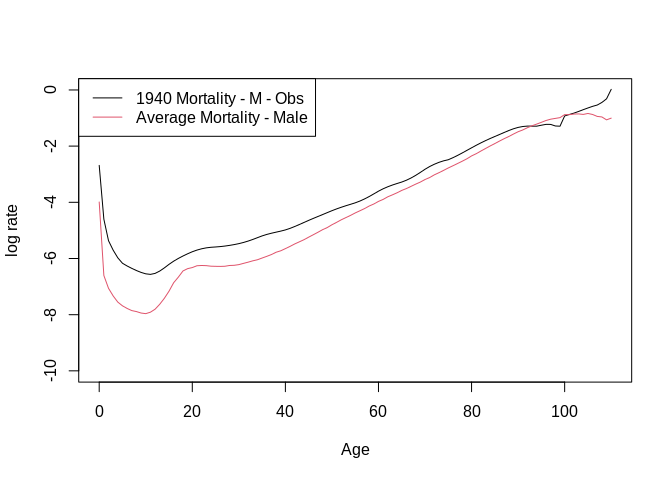
# plotting mortality for Age = 60 as a trial run to see if code is working
# as exxpected
plot(x = Years, y = m_mat[60,], pch = 18, xlab = "Years", ylab = "log m", col = 2,
main="Age 60 mortality over time") #working!!!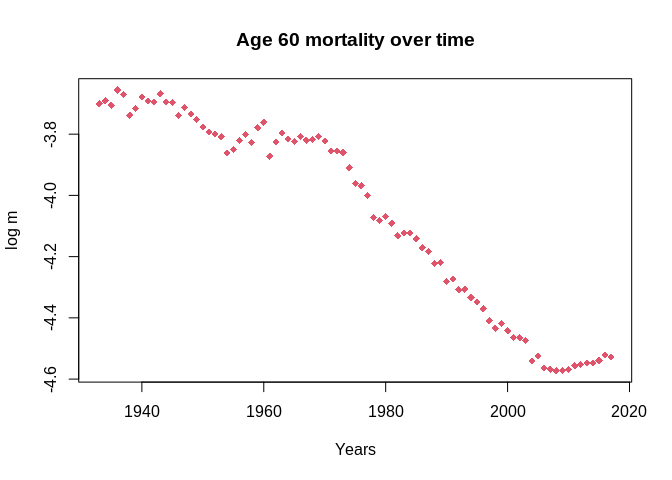
# LC with StMoMo-----
# Extracting male and female dat from HMD, after creating a StMoMo data object
# "Male" and "Female" data are assigned to different variables for easier
# data wrangling.
library(colorspace)
library(gridExtra)##
## Attaching package: 'gridExtra'## The following object is masked from 'package:dplyr':
##
## combine##
## ********************************************************## Note: As of version 1.0.0, cowplot does not change the## default ggplot2 theme anymore. To recover the previous## behavior, execute:
## theme_set(theme_cowplot())## ********************************************************library(RColorBrewer)
#Under a Binomial setting
#Becasue I'm opting to use the data with the Lee-Carter model under a Binomial setting
#the exposures have to be converted to the initial exposures.
LC1 <- lc(link = "logit")
data_m <- central2initial(usdat2_m)
data_f <- central2initial(usdat2_f)
ages_fit <- 20:60
#This can be ussed ot generate a weight matrix over the ages and years in the data.
# clips = 1 assigns 0 weights to the first and last cohorts.
wxt_m <- genWeightMat(ages = ages_fit, years = data_m$years,
clip = 1)
wxt_f <- genWeightMat(ages = ages_fit, years = data_f$years,
clip = 1)
#For males
LCfit_m <- fit(LC1, data = data_m, ages.fit = ages_fit, wxt = wxt_m)## StMoMo: The following cohorts have been zero weigthed: 1873 1997
## StMoMo: Start fitting with gnm
## Initialising
## Running start-up iterations..
## Running main iterations.........
## Done
## StMoMo: Finish fitting with gnm## StMoMo: The following cohorts have been zero weigthed: 1873 1997
## StMoMo: Start fitting with gnm
## Initialising
## Running start-up iterations..
## Running main iterations........
## Done
## StMoMo: Finish fitting with gnm#plotting parameters
par(mfrow = c(1,3))
plot(x = ages_fit, y = LCfit_m$ax, col = 2, type = "l", ylim=c(-10, -3), main="ax") #males
lines(x = ages_fit, y = LCfit_f$ax, col = 4) #females
plot(x = ages_fit, y = LCfit_m$bx, col = 2, type = "l", ylim=c(0, .04), main="bx")
lines(x = ages_fit, y = LCfit_f$bx, col = 4)
plot(x = usdat2_m$years, y = LCfit_m$kt[1,], col = 2, type = "l", ylim=c(-25,40), main="kt")
lines(x = usdat2_m$years, y = LCfit_f$kt[1,], col = 4)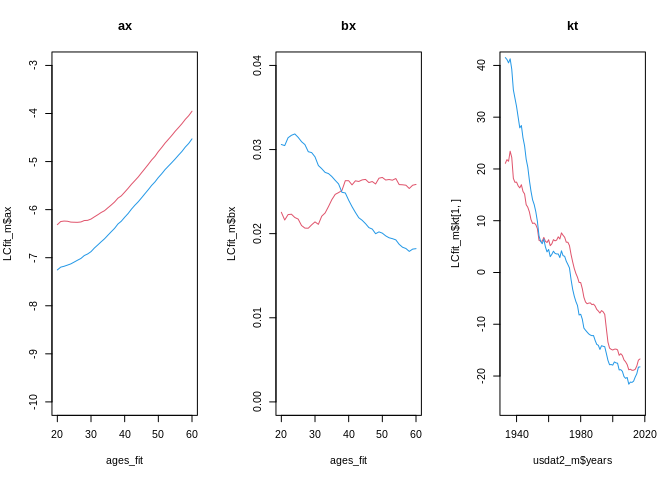
#Goodness-of-fit analysis-----
# For males
res_m <- residuals(LCfit_m)
aic_ <- AIC(LCfit_m)
bic_ <- BIC(LCfit_m)
aic_## [1] 194351.5## [1] 195367.2#For females
res_f <- residuals(LCfit_f)
#Plotting colour maps of males and females
p1 <- plot(res_m, type = "colourmap", main = "Residuals of Male data")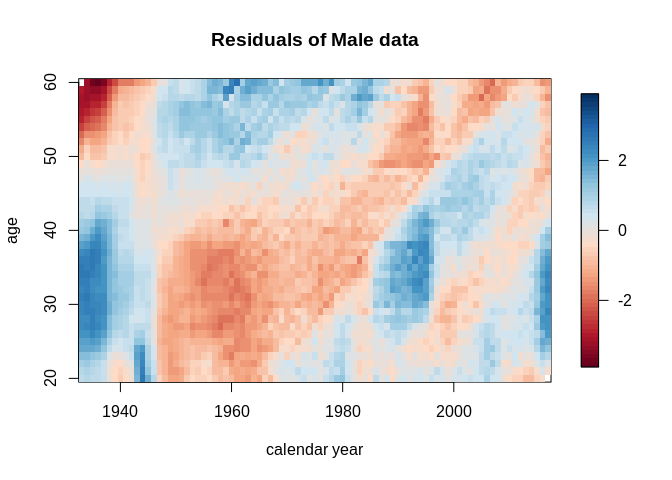
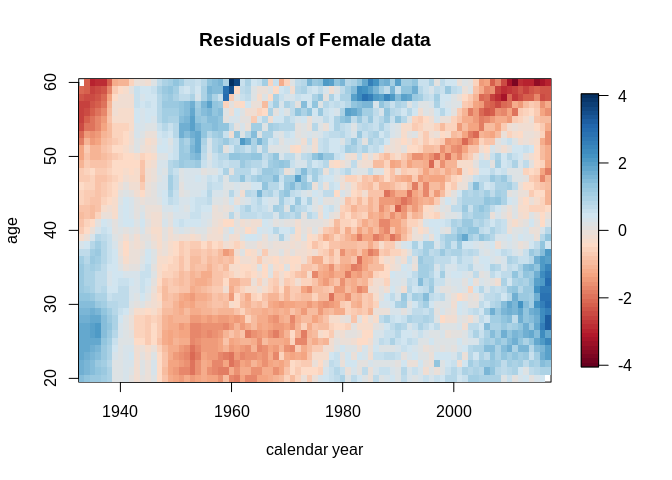
Ok, actual forecast
#Forecasting----
LCfore_m <- forecast(LCfit_m, h = 50)
LCfore_f <- forecast(LCfit_f, h = 50)
## Comparison of forcasting done in three instances:
# a.) Forecasting kt with random walk using the forecast funciton.
# b.) Forecast of kt done with SVD and first principles.
# c.) Forecast of kf done with forecast and iarima.
par(mfrow=c(1,2))
plot(x = LCfit_m$years, y = LCfit_m$kt[1,], type = "l",
ylim=c(-60, 30), xlim=c(min(usdat2_m$years),max(LCfore_m$years)),
main="kt for males - forecast",
ylab = "kt")
lines(x = LCfore_m$years, y = LCfore_m$kt.f$mean, col = 2)
lines(x = LCfore_m$years, y = LCfore_m$kt.f$upper[1,,1], col = 4)
lines(x = LCfore_m$years, y = LCfore_m$kt.f$lower[1,,1], col = 4)
plot(x = LCfit_m$years, y = LCfit_f$kt[1,], xlab = "Years",type = "l",
ylim=c(-60, 30), xlim=c(min(usdat2_m$years),max(LCfore_m$years)),
main="kt for females - forecast",
ylab = "kt")
lines(x = LCfore_m$years, y = LCfore_f$kt.f$mean, col = 2)
lines(x = LCfore_m$years, y = LCfore_f$kt.f$upper[1,,1], col = 4)
lines(x = LCfore_m$years, y = LCfore_f$kt.f$lower[1,,1], col = 4)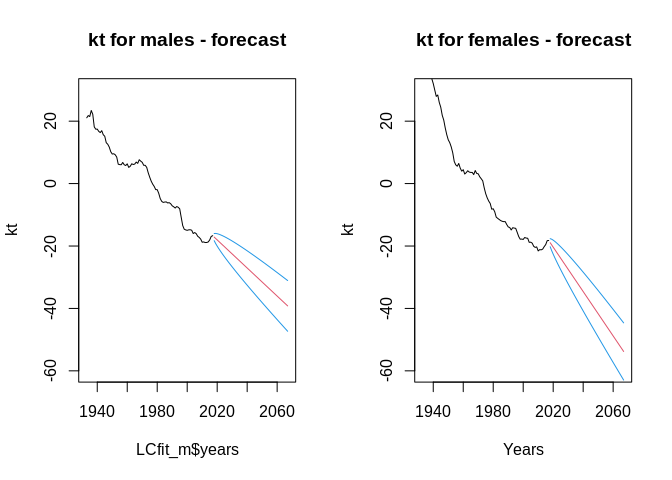
## Warning in fit.StMoMo(lc(link = "logit"), data = usdat2_m, ages.fit = 30:80): logit-Binomial model fitted to central exposure data## StMoMo: Start fitting with gnm
## Initialising
## Running start-up iterations..
## Running main iterations.........
## Done
## StMoMo: Finish fitting with gnm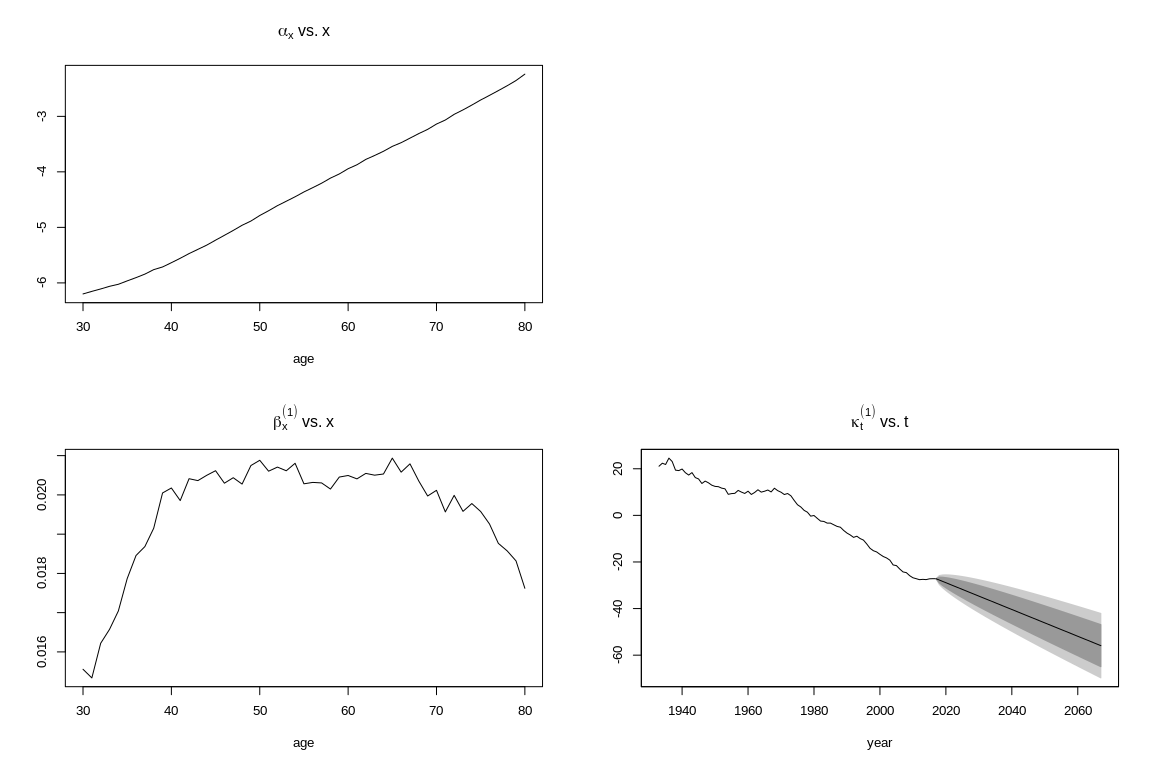
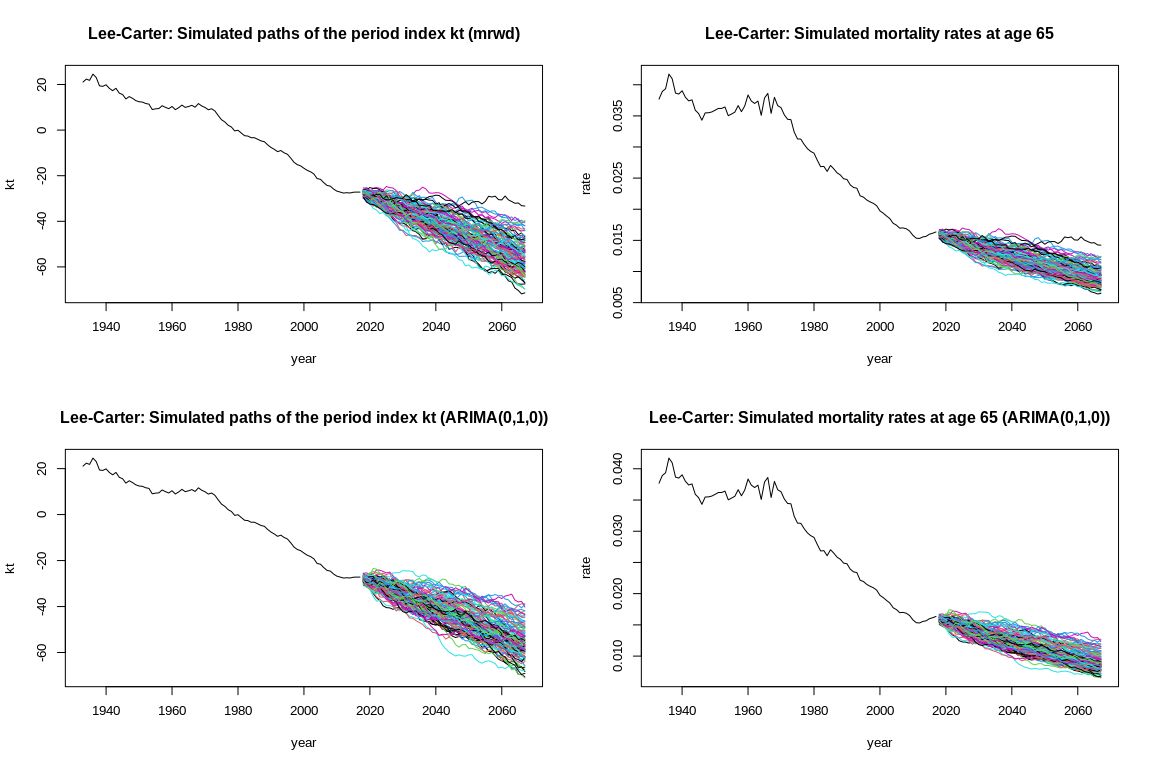
#More simulations
LCsim.mrwd <- simulate(LCfit, nsim = 100)
LCsim.iarima <- simulate(LCfit, nsim = 100, kt.method = "iarima")
par(mfrow=c(2, 2))
plot(LCfit$years, LCfit$kt[1, ], xlim = range(LCfit$years, LCsim.mrwd$kt.s$years),
ylim = range(LCfit$kt, LCsim.mrwd$kt.s$sim), type = "l",
xlab = "year", ylab = "kt",
main = "Lee-Carter: Simulated paths of the period index kt (mrwd)")
matlines(LCsim.mrwd$kt.s$years, LCsim.mrwd$kt.s$sim[1, , ], type = "l", lty = 1)
plot(LCfit$years, (LCfit$Dxt / LCfit$Ext)["65", ],
xlim = range(LCfit$years, LCsim.mrwd$years),
ylim = range((LCfit$Dxt / LCfit$Ext)["65", ], LCsim.mrwd$rates["65", , ]),
type = "l", xlab = "year", ylab = "rate",
main = "Lee-Carter: Simulated mortality rates at age 65")
matlines(LCsim.mrwd$years, LCsim.mrwd$rates["65", , ], type = "l", lty = 1)
plot(LCfit$years, LCfit$kt[1, ], xlim = range(LCfit$years, LCsim.iarima$kt.s$years),
ylim = range(LCfit$kt, LCsim.iarima$kt.s$sim), type = "l",
xlab = "year", ylab = "kt",
main = "Lee-Carter: Simulated paths of the period index kt (ARIMA(0,1,0))")
matlines(LCsim.iarima$kt.s$years, LCsim.iarima$kt.s$sim[1, , ], type = "l", lty = 1)
plot(LCfit$years, (LCfit$Dxt / LCfit$Ext)["65", ],
xlim = range(LCfit$years, LCsim.iarima$years),
ylim = range((LCfit$Dxt / LCfit$Ext)["65", ], LCsim.iarima$rates["65", , ]),
type = "l", xlab = "year", ylab = "rate",
main = "Lee-Carter: Simulated mortality rates at age 65 (ARIMA(0,1,0))")
matlines(LCsim.iarima$years, LCsim.iarima$rates["65", , ], type = "l", lty = 1)